The average height of a wall

HOME

Math Central

Quandaries & Queries

Question from Jeff:

Trying to figure the average height of a sloped foundation wall.
The lowest point is 24 inches or 2 feet.
The highest point is 116 inches or 9’ 8 inches.
Can this be figured without the degree of slope or can we assume it is
Equaled sloped from point a to point b. Thanks

Hi Jeff,

I drew a diagram of the face of your wall. The height at the point $P$ is 24 inches and the height at point $R$ is 116 inches.

wall

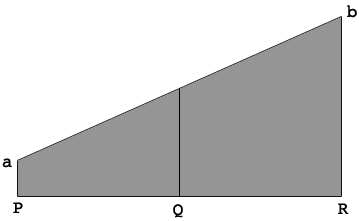
$Q$ is midway from $P$ to $Q.$ Since the top of the wall is a straight line from $a$ to $b$ the average height is the height at $Q$ which is the average of the height at $P$ and the height at $R.$ Hence the average height is

\[\frac{24 + 116}{2} = 70 \mbox{ inches.}\]

As a justification I drew a red horizontal line 70 inches above the base.

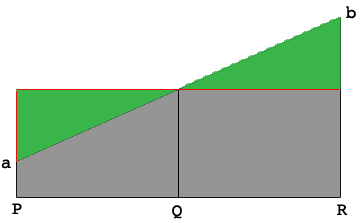
wall 2

Notice that the two green triangles are identical (congruent)

I hope this helps,
Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.