| |||
| Math Central | Quandaries & Queries |
|
Question from Kirklan: Jeremy wants to construct an open box from an18-inch square piece of aluminum. He plans to cut equal squares, with sides of x inches, from each corner and then fold each side up to form the box. If Jeremy wants the volume of the box to be 432 cubic inches, what should the minimum length of the sides of the squares cut from each corner be? Find the volume, V, of the box as a function of x. Given: V = length × width × height. |
Hi Kirklan,
Here is my diagram of the sheet of aluminum with the 4 corner squares of side length $x$ inches, ready to be cut out.
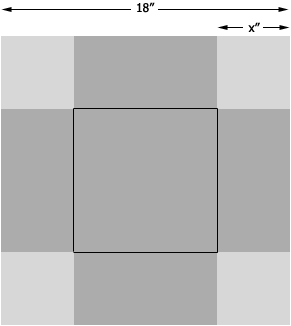
After the corner squares are cut out the aluminum is folded up along the black lines to form a box.
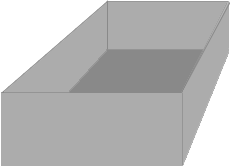
What is the length of the box? What is its width? what is its height? What is its volume?
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.