Hi Mary,

I drew a diagram of your flat top cone (truncated cone), extended it to a full cone, and added some labels. My diagram is not to scale.

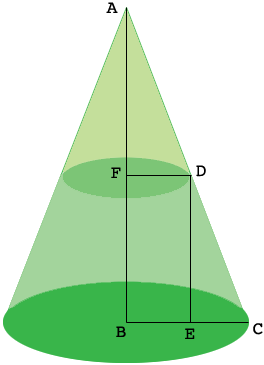
$|BC| = 12.5 \mbox{ cm, } |FD| = 7 \mbox{ cm, and }|ED| = 15 cm.$ Hence $|EC| = 5.5 \mbox{ cm.}$ Triangle $DEC$ is a right triangle so Pythagoras' Theorem gives us

\[|CD|^2 = |DE|^2 + |EC|^2 = 225 + 30.25 = 255.25 \mbox{ so } |CD| = 16.89 \mbox{ cm.}\]

Triangles $ABC$ and $DEC$ are similar and hence

\[\frac{|CA|}{|BC|} = \frac{|CD|}{|EC|} \mbox{ and hence } |CA| = 38.39 \mbox{ cm.}\]

Thus $|AD| = 38.39 - 16.89 = 21.50 \mbox{ cm.}$

Imagine that you slice the surface of the cone along the line $CA$ and roll it out flat to form a sector of a circle.

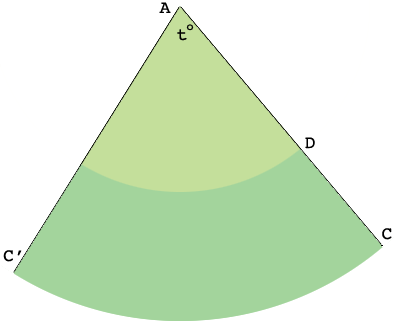
There are two copies of $C$ on the rolled out image, and I called one of them $C^{\prime}.$

The length of the arc from $C$ to $C^\prime$ is the circumference of the circular base of the cone so the length is $2 \times \pi \ 12.5$ cm. This arc is a fraction of the circumference of the circle with centre $A$ and radius $|AC|.$ Likewise the measure of the angle $t^o$ at the center of the sector is a fraction of $360^{0},$ the angle all the way around the circle. By the symmetry of a circle these fractions are the same. Thus

\[\frac{2 \times \pi \ 12.5}{2 \times \pi \ 38.39} = \frac{t^o}{360^o}\]

and hence

\[t^o = 117.2^{o}.\]

I hope this helps,
Penny