y=lnx+(1+ln2)/2 and y=x^2

HOME

Math Central

Quandaries & Queries

Question from Mike:

Prove that y=lnx+(1+ln2)/2 and y=x^2 touch each other.

The course is about logarithm and root functions... how should I solve this problem?

Hi Mike,

I wasn't sure what was meant by "touch each other" so I plotted the two functions

\[f(x) = \ln(x) + \frac{1 + \ln(2)}{2} \mbox{ and } g(x) = x^{2}.\]

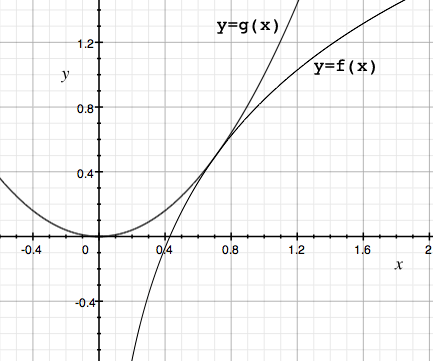
graph

It does look like the two curves have a common tangent at approximately x = 0.7. If they do have a common tangent there then at this point we would have

\[f^\prime (x) = g^\prime (x).\]

Can you finish it?
Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.