Hi,

I think you know that the volume $V$ of a cone in cubic centimeters is given by

\[V = \frac{1}{3} \pi \; r^2 h\]

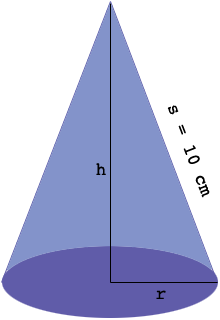
where $r$ is the radius of the cone and $h$ is its height, both in centimeters. I am assuming this problem comes from a calculus class where you are learning about finding the maximum and minimum of a function of one variable. Unfortunately $V$ above is a function of two variables, $r$ and $h.$ You do however know one further fact, the slant height $s$ is $s = 10$ centimeters. If you can use this to find a relationship involving $r$ and $h$ perhaps you can solve it for $r$ in terms of $h,$ substitute into the expression for $V$ giving $V$ as a function of $h$ alone. This will allow you to use the calculus you know to maximize $V.$

To find a relationship involving $r$ and $h$ maybe a diagram will help.

Penny