| |||
| Math Central | Quandaries & Queries |
|
Question from Remo: So, little game my kid came up with. Dice are standard d6. I roll a die, he rolls a die. If he gets the same number as me OR a bigger number he wins. Then we upped the ante. Then again we upped. |
Hi Remo,
Below is the table you sent with instructions on how to read it.
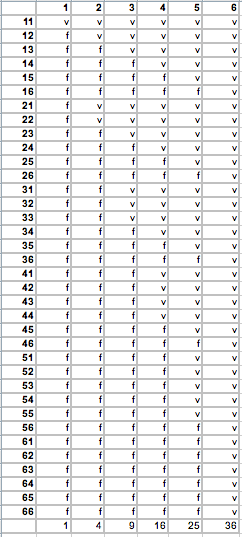
I got a sheet with the tabled result I figured with him:
upper column is what he rolls, side is what I roll on either dice (34 is one dice 3, one 4). v is for his victory, f for when he fails. The probability of victory is then \[\frac{1 + 4 + 9 + 16 + 25 + 36}{216} = \frac{91}{216}.\]
My approach is slightly different and I hope it can be extended to the case where you both roll two dice.
The results of you rolling dice and your son rolling dice are independent events. That is the result of either of your rolls has no influence on the result of the other's rolls. If $A$ and $B$ are independent events and $Pr(A)$ is the probability of $A$ and $Pr(B)$ is the probability of $B$ then
\[Pr(A \mbox{ and }B) = Pr(A) \times Pr(B).\]
For your son rolling two dice there are 6 possible outcomes and each has probability $\large \frac1{6}.$
You roll two dice and record the larger of the two dice. Again there are 6 possible results and I used a table to calculate the probabilities. The rows represent the result on your first die and the columns the result on your second die. In the body of the table is the larger of the two results.
1 |
2 |
3 |
4 |
5 |
6 |
|
|---|---|---|---|---|---|---|
| 1 | 1 |
2 |
3 |
4 |
5 |
6 |
| 2 | 2 |
2 |
3 |
4 |
5 |
6 |
| 3 | 3 |
3 |
3 |
4 |
5 |
6 |
| 4 | 4 |
4 |
4 |
4 |
5 |
6 |
| 5 | 5 |
5 |
5 |
5 |
5 |
6 |
| 6 | 6 |
6 |
6 |
6 |
6 |
6 |
The probability of ending in any particular cell in the table so each has probability $\large \frac{1}{36}.$ Hence the probability of the larger being 1 is $\large \frac{1}{36},$ the probability of the larger being 2 is $\large \frac{3}{36},$ the probability of the larger being 3 is $\large \frac{5}{36}$ and so on.
Hence for rolling two dice and recording the larger number on the dice I get
| Larger of the two dice | Probability |
|---|---|
| 1 | 1/36 |
| 2 | 3/36 |
| 3 | 5/35 |
| 4 | 7/36 |
| 5 | 9/36 |
| 6 | 11/36 |
Finally one last table. Here the rows represent the result of your son rolling 1 die and the columns represent the larger of the two dice you roll. In the body of the table I have V for a victory by your son and F for a failure.
1 |
2 |
3 |
4 |
5 |
6 |
|
|---|---|---|---|---|---|---|
| 1 | V |
F |
F |
F |
F |
F |
| 2 | V |
V |
F |
F |
F |
F |
| 3 | V |
V |
V |
F |
F |
F |
| 4 | V |
V |
V |
V |
F |
F |
| 5 | V |
V |
V |
V |
V |
F |
| 6 | V |
V |
V |
V |
V |
V |
Look at a particular place in the table, for example when you son rolls a 3 and your larger die is a 2. The probability of that result is
\[Pr(\mbox{ your son rolls a 3 and your larger is a 2 }) = Pr(\mbox{ your son rolls a 3 }) \times Pr(\mbox{ your larger is a 2 }) = \frac{1}{6} \times \frac{3}{36} = \frac{3}{36}.\]
Another example, when your son rolls a 4 and your larger die is 5 the probability is
\[Pr(\mbox{ your son rolls a 4 and your larger is a 5 }) = Pr(\mbox{ your son rolls a 4 }) \times Pr(\mbox{ your larger is a 5 }) = \frac{1}{6} \times \frac{9}{36} = \frac{9}{36}.\]
Calculate the probability for each of the V cells and add then to get the probability that your son is the victor.
Can you see now how to use my technique or a combination of our techniques to find the probability when you both roll two dice?
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.