Hi Rob,

I labeled the corners of your lot from $A$ to $E,$ added two points $F$ and $G,$ and two lines perpendicular to $AB.$

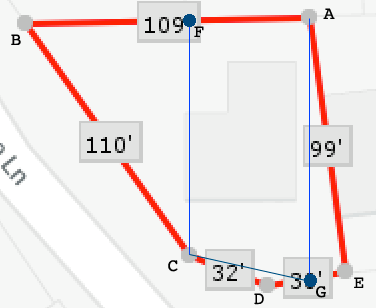
I printed your page and measured the lengths $|EA|$ and $|AB|$ in millimeters and got $|EA| = 73$ mm and $|AB| = 81$ mm. I used both of these to calculate a scale and found that

\[\frac{99}{73} = 1.36 \mbox{ and } \frac{109}{8} = 1.36\]

and hence I am convinced that the scale in the horizontal and vertical direction is 1.36 feet to 1 mm.

I then measured $|FB|$ to be 46 mm so my estimate of the distance from $B$ to $F$ on your lot is $1.36 \times 46 = 61.9$ feet. I then measured $|FC|$ to be 66 mm so the distance from $F$ to $C$ on your lot is $1.36 \times 66 = 89.76$ feet. Thus the area of triangle $FBC$ is

\[\frac{89.76}{2} \times 61.9 = 2778.072 \mbox{ square feet.}\]

Similarly I measured $|GE|$ to be 10 mm so the distance from $G$ to $E$ is $1.36 \times 10 = 13.6$ feet. And again $|EG|$ measures 73 mm so the distance from $A$ to $G$ is 98.28 feet. I then assumes that the angle $AEG$ is a right angel (it looks close) so the area of triangle $AGE$ is

\[\frac{98.28}{2} \times 13.6 = 675.104 \mbox{ square feet.}\]

The distance from $F$ to $A$ is $109 - 61.9 = 47.1$ feet and hence the trapezoid $AFCG$ has area

\[\frac{89.76 + 98.28}{2} \times 47.1 = 4428.5775 \mbox{ square feet.}\]

The sum of the areas of the triangles $FBC, ADE$ and the trapezoid $AFCG$ is 7882 square feet. This is approximately the area of your lot. It leaves out the triangle $GCD$ but I think that is quite small.

This is the best I can do with the information I have. I hope it helps,
Harley