| |||
| Math Central | Quandaries & Queries |
|
Question from Sameer: Bottom cone radius 1124.hight is 200. Top radius 15degree decrease to bottom radius. Top radius how much ? |
Hi,
Below is my sketch the situation you described. My sketch is not to scale. $AB$ is the radius of the base circle so $|AB| = 1124$ units. The height $|AE| = |BD| = 200$ units and the radius $|EC|$ of the top circle is unknown. I'm going to call it $R$ units. The measure of the angle $BCD$ is 15 degrees.
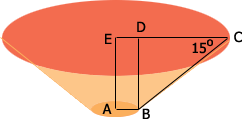
The length of $ED$ is 1124 units so the length of $DC$ is $R - 1124$ units. The triangle $BCD$ is a right triangle and hence
\[ \tan(15^o) = \frac{|BD|}{|DC|} = \frac{200}{R-1124}.\]
Thus
\[R - 1124 = \frac{200}{\tan(15^o} = \frac{200}{0.2679} = 746.4.\]
Hence
\[R = 1124 + 746.4 = 1870.4 \mbox{ units.}\]
Penny
 |
||
| * Registered trade mark of Imperial Oil Limited. Used under license. | ||
Math Central is supported by the University of Regina and the Imperial Oil Foundation.