Hi Tom,

Here is a diagram of one such triangle.

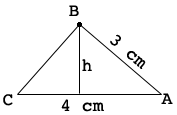
It's area is

\[\frac12 \times 4 \times h \mbox{ square centimeters.}\]

In my second diagram the orange curve is an arc of a circle with center $A$ and radius 3 cm.

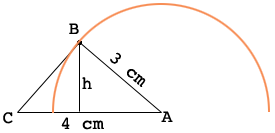
The point $B$ must be on this arc if the length of $AB$ is 3 cm. What point on the arc makes $h$ a maximum and hence gives a triangle of maximum area?

Penny