Hi,

The notation $f(x)$ or $y = f(x)$ is used to describe a function. I'm going to think of a function as a process or procedure that accepts a number as its input and generates a number as its output. For example the square function that accepts a number as its input and outputs the square of the number. Thus inputting $3$ produces $3^2 = 9$ and inputting $2.5$ yields $6.25.$

In the notation $y = f(x),$ the input is $x,$ the output is $y$ and the name of the function is $f.$ Here is an example using a calculator. Below is an image of the calculator of my computer.

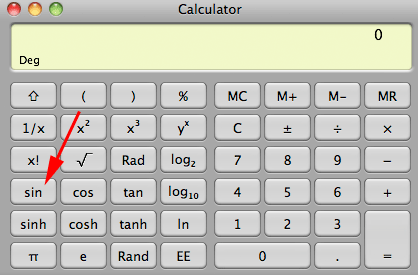
The function I want to use is the sine function so using the $y = f(x)$ notation, $f = sin.$ I want to input $30^o$ to the sine function so $x = 30.$ Hence I type $30$ on the calculator keypad, activate the function by pressing the $sin$ button and the calculator displays $0.50$ which means $y = 0.50.$ hence using the function notation $y = f(x)$ becomes $0.5 = sin(30).$

Functions are much more general then this. Neither the input nor the output needs to be a number.

Write back if you have more questions,
Penny