Hi Barbie,

I drew a diagram of the example you sent (not to scale) as I understand it. Let me know if I have something incorrect.

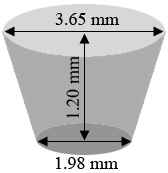
You are correct, this is a frustum of a cone.

I am going to extend the diagram to form the full cone and a some labels.

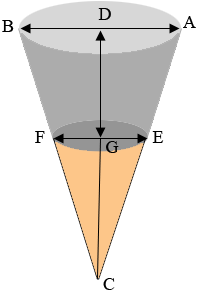
I wasn't sure which angle you were looking for but from a page on Wikepedia I think it is the angle $BCA.$

Let the distance from $G$ to $C$ be $x$ mm. Triangles $BCA$ and $FCE$ are similar so

\[\frac{|AB|}{|DC|} = \frac{|EF|}{|GC|} \mbox{ or for your example } \frac{3.65}{1.2 + x} = \frac{1.98}{x}.\]

Simplifying the expression for the example gives

\[3.65 \times x = 1.98 \times {(1.2 + x)}\]

or

\[(3.65 \times x = 2.376 + 1.98 \times x.\]

This gives $x = 1.4228$ mm.

But the tangent of the angle $DCA$ is $\large \frac{|AB|/2}{|DC|}.$ For your example this gives

\[\tan(DCA) = \frac{3.65/2}{1.20 + 1.4228} = 0.6958\]

and hence the measure of the angle $DCA$ is

\[\tan^{-1}(0.6958) = 34.8^{o}\]

and the measure of angle $BCA$ is $2 \times 34.8 = 69.6^{o}.$

You were expecting $90^{o}.$ Is my diagram incorrect? do you see an error in my calculations?

Hariey