Hi Callie,

I drew a diagram of your hexagonal planter and added lines joining the opposite corners. The six triangles formed all meet at the center $C$ of the planter. The six angles formed at $C$ have equal measurements so each measures $\large \frac{360}{6} \normalsize = 60$ degrees.

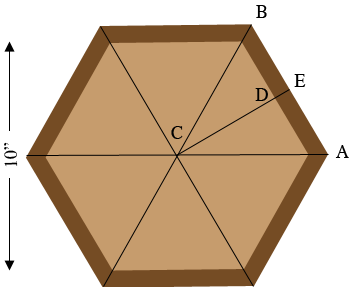
Since the distance from $B$ to $C$ is equal to the distance from $A$ to $C$ all three interior angles of the triangle $ABC$ are equal and hence the angle $CAB$ measures $60^{o}.$ If the distance from $A$ to $B$ is 6 inches then the interior width of the planter will be approximately 10 inches as indicated in the diagram. Thus for the hexagonal planter cut 6 pieces, each 6 inches long at a $60^o$ angle.

For an octagonal planter the cut 8 pieces, 5.5 inches long at an angle of $67.5^{o}.$

I hope this helps,

Harley

Callie wrote back

Good Morning, Well I have another question. My saw only goes to 45 angle. What's the trick to cutting the 60 degree angle you said to cut this hexagon. Thank you!

And if I wanted an interior of 12", what length do I cut each 2x4?

If you set the saw angle to $30^o$ and cut the board as in the diagram below then the angle at the heal of the cut measures $90^o + 30^o = 120^{o}$ and the angle at the toe, angle $CAB$ in the first diagram, measures $60^{o}.$

In the first diagram $E$ is the midpoint of $AB$ and the dark brown piece from $A$ to $B$ is a 2 by 4 on its side. Hence the distance from $D$ to $E$ is 3.5 inches. Suppose the distance from $C$ to $D$ is $x$ inches then the distance from $A$ to $E$ is

\[\frac{x + 3.5}{\sqrt 3} \mbox{ inches.}\]

If you want the interior dimension to be 12 inches then $x = 6$ inches and

\[\frac{x + 3.5}{\sqrt 3} = \frac{9.5}{\sqrt 3} = 5.48 \mbox{ inches.}\]

Thus the distance from $A$ to $B$ is $2 \times 5.48$ which is about 11 inches.

Harley