Hi Colleen,

In my diagram $C$ is the center of the hexagon and the square. Hence $|CD| = 16$ inches and the measure of the three interior angles of the triangle $AEC$ is $60^{o}.$ Hence triangle $AEC$ is an equilateral triangle and the side length of the hexagon is $|AE| = |CA|.$

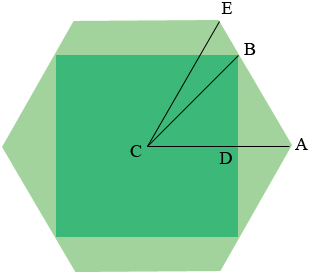
By the symmetry in the diagram angle $BDA$ is a right angle and hence triangle $BDA$ is a right triangle and

\[\frac{|BD|}{|DA|} = \tan(\left(60^o\right) = \sqrt{3}.\]

Thus

\[|DA| = \frac{|BD|}{\sqrt{3}} = \frac{16}{\sqrt{3}} = 9.24.\]

Hence the side length of the hexagon is $|CA| = |CD| + |DA| = 16 + 9.24 = 25.24$ inches.

I hope this helps,
Penny