Hi Ella,

In my diagram the sector shaded red is cut out and removed and the remaining sector, shaded green, is used to form the cone. The sector angle of the red sector measures $\theta$ radians an thus the sector angle of the green sector measures $2 \pi - \theta$ radians. The length of the arc that borders the green sector has length $2 \pi - 42 \theta$ cm.

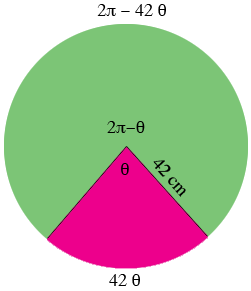
The cone formed has volume $V = \large \frac{1}{3} \normalsize \pi r^2 h$ cubic centimeters using the notation in the diagram below. This expression is a function of $r$ and $h$ but if you can express $r$ and $h$ in terms of $\theta$ you can use the calculus you know to maximize $V$ as a function of $\theta.$

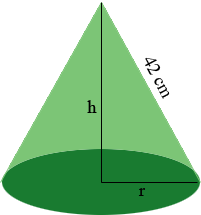
The dark green base is a circle of radius $r$ and its circumference is the arc that borders the green sector has length $2 \pi - 42 \theta$ cm in the first diagram. The circumference if a circle of radius $r$ cm is $2 \pi r$ cm and hence you can express $r$ in terms of $\theta.$ The triangle with sides of length $r, h$ and 42 cm in the diagram above is a fight triangle and hence you can use Pythagoras Theorem to express $h$ in terms of $r$ and hence in terms of $\theta.$

I hope this helps,
Penny