Hi Faisal,

I drew a diagram of what you described. $C$ with coordinates $(h,k)$ is the center of the circle, $b$ is the point on the circle with coordinates $(5, -16)$ and $A$ is the point where the X-axis is tangent to the circle.

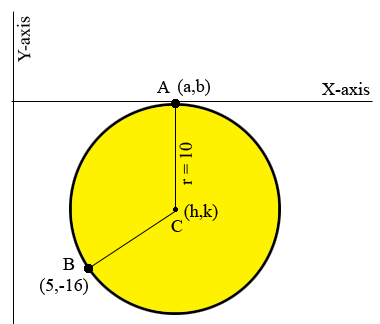
I gave $A$ the coordinates $(a,b)$ but since $A$ is on the X-axis $b = 0.$ The tangent line and the line segment $AC$ form a right angle and hence $k = -10.$ The length of $BC$ is 10units so

\[(h-5)^2 + (k+16)^2 = 10^{2}.\]

But $k = 0.$

Solve for $h$ and write the equation of the circle.

Is there another diagram for the situation you described?

Penny