Hi Isaac,

The feasible region, the region of the plane that satisfies all the inequalities, is described by the inequalities. Since $x$ and $y$ must both be non-negative we have that $0 \le x \le 4$ and $y \ge 11.$ Hence the feasible region so far is strip of the plane between or on the vertical lines $x = 0$ and $x = 4$ and above or on the horizontal line $y = 11.$ Draw a graph of the plane highlights this region.

Since the number of coins is no more than 15 we know that $x + y \le 15.$ I would add this restriction by first adding the line $x + y = 15$ to the graph you have.

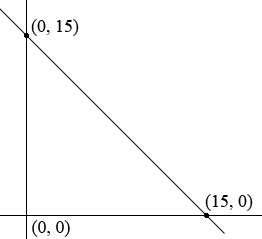
This line partitions the plane into three regions, the points on the line, the points above the line, and the points below the line. The points in the plane that satisfy $x + y \le 15$ are the points on the line and all the points in one of the other two regions. To determine which one choose a point in one of the other regions, I am going to choose $(0, 0),$ and determine whether it satisfies the inequality. It does, so all the points on the line and below the line satisfy $x + y \le 15.$ How does this modify the feasible region you have so far?

You have one more restriction the coins are "worth a minimum of $\$1$ combined". I am going to work in cents rather than dollars. Each nickel is worth 5 cents and each dime is worth 10 cents s this last restriction can be written $5x + 10y \ge 100.$ Does this restriction make any change to the feasible region?

Write back if you have any further questions,
Penny