Vectors - Math Central

HOME

Math Central

Quandaries & Queries

Question from Kayla:

Hi!
Due to time constraint issues, we skipped vectors in Pre-Calc last year. However, I'm attempting to complete my AP Physics summer homework and there are 3 problems with vectors. As I explained, I have no idea even where to begin and as such I need some help.

Problem 1:
A plane flying at 90° at 45 m/s is blown toward 0° at 62 m/s by a strong wind. Find the plane's resultant velocity.
I have tried all sorts of online calculators but none are providing me with a formula I can use to solve this problem on my own.

Problem 2:
If you walk 367 m North and 785 m West what is your total displacement from your original location?
What is the problem asking for when it says displacement?

Problem 3:
A plane travels on a heading of 127.0° at a velocity of 25 km/hr. What are the horizontal and vertical components of the plane's velocity?
As you know already, I have never done vectors so I don't know what horizontal and vertical components of velocity are.

Thank you So Much for your help!! I am struggling!!

- Kayla

Hi Kayla,

Problem 1:

I don't understand what "blown toward 0°" means. If you think of compass bearings then "flying at 90°" means you are flying directly north. Does the question say "blown at 0° at 62 m/s"?

Problem 2:

The displacement is a vector from the starting point to the ending point, so it doesn't depend on the path taken. In your problem if you start at the origin in the plane and you go 367 m north and then 785 m west you end at the point (-785, 367). What is the vector from (0,0) to (-785, 367)?

Problem 3:

I looked on the web and found

In physics, when you break a vector into its parts, those parts are called its components. For example, in the vector (4, 1), the x-axis (horizontal) component is 4, and the y-axis (vertical) component is 1.

at Physics1 for Dummies.

I drew a diagram with your vector.

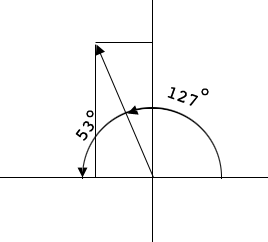
vector

Can you determine the components?

Write back if you need more assistance,
Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.