Mandy walks to work - Math Central

HOME

Math Central

Quandaries & Queries

Question from Kenneth:

Mandy walks to work at a constant rate. One-third of the way to work, she passes a bank.
Three-fourths of the way to work, she passes a book store.
At the bank her watch reads 7:52 A.M., and at the book store it reads 8:02 A.M.
At what time is Mandy one-half of the way to work?

Hi Kenneth,

I can show you a way to approach this problem and get you started. First I drew a diagram, I almost always draw a diagram.

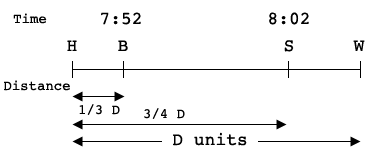
diagram

H is home, B is the bank, S is the book store and W is work.

On the time scale Mandy is at B at 7:52 and at S at 8:02. Thus it takes her 10 seconds to go from B to S.

For distance I let the distance from H to W be D units. Thus the distance from B to S is

\[\frac{3}{4} D - \frac{1}{3} D = \frac{5}{12} D.\]

Hence Mandy goes a distance of $\large \frac{5}{12} \normalsize D$ units in 10 seconds.

I'm sure you can do the rest,
Harley

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.