Hi Lauchie,

In my diagram below the octagon is divided into 8 triangles, each with a vertex at the center $C$ of the octagon. The 8 angles at $C$ have the same measure and hence the measure of each is $\large \frac{360^o}{8} \normalsize = 45^{0}.$

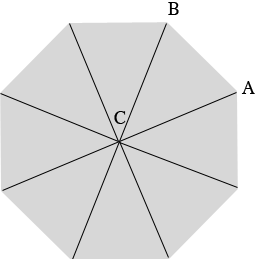
Using the facts that the triangle $ABC$ is isosceles and that the sum of the angle measures in a triangle is $180^{o}$ you can show that the angle $CAB$ measures $67.5^{o}.$ Hence each of the angle cuts is $67.5^{o}.$

I redrew the diagram and added a point $D$ midway between $A$ and $B.$

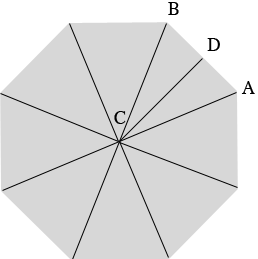
You said that the pool is a 24 foot round pool so the diameter of the pool is 24 feet and its radius in thus 12 feet. When you put the octagonal deck around the pool I don't know if you want $|AC|,$ the length of the line from $A$ to $C$ to be 12 feet or $|DC|.$ the length of the line from $D$ to $C$ to be 12 feet.

|DC| = 12 feet:

\[\tan\left(CAD\right) = \tan\left(67.5^o\right) = 2.414 = \frac{|DC|}{|AD|} \]

so

\[|AD| = \frac{12}{2.414} = 4.97 \mbox{ feet.}\]

and thus $|AB| = 2 \times 4.97 = 9.9$ feet which is 9 feet 9 inches.

|AC| = 12 feet:

\[\cos\left(CAD\right) = \cos\left(67.5^o\right) = 0.383 = \frac{|AD|}{|AC|} \]

so

\[|AD| = 0.383 \times 12 = 4.59 \mbox{ feet.}\]

and thus $|AB| = 2 \times 4.59 = 9.2$ feet which is 9 feet 2 inches.

I hope this works for you,
Harley