Hi Maria,

Are thinking of a shape something like this? (My diagram is not to scale.)

Penny

Maria wrote back

Hi Penny,

Thanks for your prompt reply and yes indeed the shape you show is
indicative of what I mean.

Regards,

Maria

Hi Maria,

I added some labels and dimensions to my drawing.

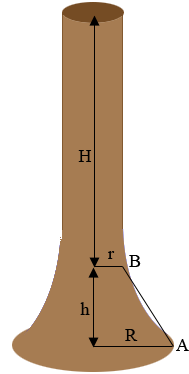
$R$ is the radius of the base of the tree and $r$ is the radius of the trunk. $A$ is a point on the ground at the base of the tree and $B$ is a point on the tree where the sloped base meets the main trunk. The vertical distance between $A$ and $B$ is $h.$ The height of the main trunks $H.$ All the measurements are in the same units..

The main trunk is a circular cylinder of radius $r$ units and height $H$ units so its volume is $\pi; r^2 h$ cubic units. Since I don't know the equation of the curve along the base from $A$ to $B$ I am going to assume it is a straight line. The base of the tree is then approximately a truncated cone.

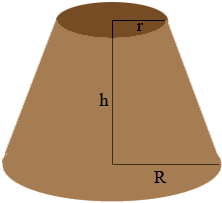
The volume of this truncated cone is

\[\frac{1}{3} \pi \; h \left(R^2 + r R + r^2\right) \mbox{ cubic units.}\]

Hence the volume of the tree is approximately the sum of the volume of the cylindrical trunk and the volume of the base.

I hope this works for you,
Penny