Hi Michael,

I drew a diagram of height of the football in yards against time in seconds and put on the information you know.

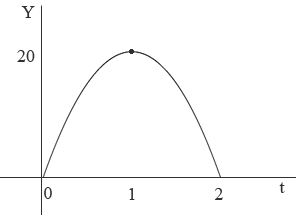
This is a parabola so its equation is

\[y = a t^2 + bt + c\]

for some constants a, b and c. Since a parabola is symmetric around its vertex so the height of 20 yards occurs when t = 1 second. You know that y = 0 when t = 0, y = 0 when t = 2, and y = 20 when t = 1. These facts allow you to determine a, b and c. I expect however that you want a parabola relating x and y not t and y.

If you ignore air friction then the flight of the football in the x direction has zero acceleration so x is a linear function of t. That is for some constants c and k, $x = kt + c.$ You know that x = 20 when t = 0 and x = 50 when t = 2. These fact allow you to determine c and k.

Solve the resulting equation for t and substitute into the equation relating y and t. This gives you a quadratic equation for y in terms of x. Simplify.

Verify that the resulting equation satisfies the data give.

Write back if you need more assistance,
Penny