| |||
| Math Central | Quandaries & Queries |
|
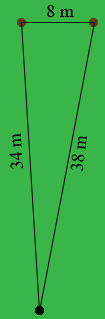
Question from Ogunjobi: Two goal post are 8m apart a footballer is 34 m from one post and 38m from the other within what angle must he kick the ball if he is to score |
Hi,
I drew a rough sketch of the situation you described.
Two very useful theorems relating to triangles are the Law of Sines and the Law of Cosines.
Suppose you have a triangle with side lengths $a, b$ and $c,$ and angle measurements $A, B$ and $C$ as in the diagram below.
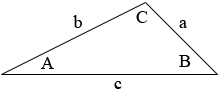
Law of Sines
\[\frac{\sin(A)}{a} = \frac{\sin(B)}{b}\]
Law of Cosines
\[c^2 = a^2 + b^2 - 2 a b \cos(C)\]
In the Law of Sines there are four variables, $a, A, b,$ and $B.$ If you know that values of any three of the variables you can solve for the fourth.
In the Law of Cosines you also have four variables, $a, b, c,$ and $C.$ Again if you know that values of any three of the variables you can solve for the fourth.
Which of the two laws can you apply to the problem you sent?
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.