Hi Richard,

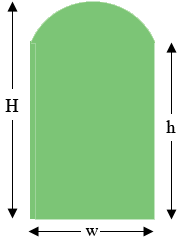
Does the diagram above depict the situation you described, where the width $w,$ the overall height $H,$ and the leg length $h,$ are known? I am assuming the arch is a section of a circle. If so can you send me $w, H$ and $h$ for a particular example and I will generate general expressions for you and use the dimensions you send for an example calculation.

Harley

Richard replied

Yes your diagram is perfect.
H = 71.5
h = 62
w = 35.5

I redid the diagram and added to it. $C$ is the center of the circle that forms the arch, $r$ is the radius of the circle, $E$ is the midpoint of the line segment $AB,$ and $y = H - h.$

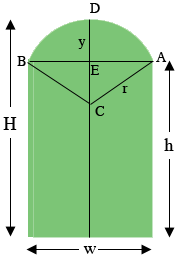
I assume your measurements are in inches.

The first task is to find the value of $r.$ Triangle $AEC$ is a right triangle so Pythagoras Theorem gives

\[|CA|^2 = |AE|^2 + |EC|^2 \mbox{ or } r^2 = \left( \frac{w}{2} \right)^2 + (r-y)^2\]

solving this expression for $r$ and simplifying gives

\[r = \frac{4 y^2 + w^2}{8 y} \mbox{ units.}\]

For the example you sent this gives

\[r = \frac{4 \times (71.5 - 62)^2 + 35.5^2}{8 \times (71.5 - 62} = 21.33 \mbox{ inches.}\]

I next need to know the measure of the angle $ACB.$ Again from triangle $AEC,$

\[\sin \left( ACE \right) = \frac{|AE|}{|CA|} = \frac{w/2}{r}\]

and hence the measure of angle $ACE$ is

\[\sin^{-1}\left( \frac{w/2}{r} \right).\]

$sin^{-1}$ is sometimes written $\arcsin$ or ASIN.

Thus the measure of the angle $ACB,$ I'm going to call it $\theta,$ is

\[\theta = 2 \times \sin^{-1}\left( \frac{w/2}{r} \right).\]

For the example you sent this gives

\[\mbox{ angle } ACB = 2 \times \sin^{-1}\left( \frac{35.5/2}{21.33} \right) = 1.966 \mbox{ radians.}\]

The length $a$ of an arc of a circle of radius $r$ and central angle $\theta$ radians is given by

\[a = r \theta.\]

Hence for your example the length of the arc $ADB$ is $21.33 \times 1.966 = 41.93$ inches.

The area of the share is the area of the rectangular part, $w \times h,$ plus the area of the circular cap $ADBC.$ The area of the circular cap is the area of the sector $ADBC$ minus the area of the triangle $ABC.$ The area of the sector is

\[\frac{1}{2} r^2 \theta\]

and the area of the circular cap $ADCB$ is

\[ \frac{1}{2} r^2 \theta - \frac{1}{2} w \times (r - y)\]

Hence the area of the shape is

\[w \times h + \left( \frac{1}{2} r^2 \theta - \frac{1}{2} w \times (r - y) \right)\]

For the example you sent this gives

\[35.5 \times 62 + \frac{1}{2} \times 21.33^2 \times 1.966 -\frac{1}{2} \times 35.5 \times (21.33 - 9.5) = 2438.2 \mbox{ square inches.}\]

If you need to convert this to square feet divide by 144.

I used an Excel Spread Sheet to verify my arithmetic I I have attached it for your use if you desire. For a different example just change the values of $H, h,$ and $w.$

Harley

Richard wrote back again

Thank you very much. I think it is great you are able to help people out like this.
Another question if you take the same shape decrease H to say 69 what is the angle where the top curve meets the side ?
This has been very challenging to figure out.

Glad to help when I can.

I modified the diagram again by inserting a coordinate system with $C$ the origin and the Y-axis through $E.$ The line $PQ$ is tangent to the circle at $B.$ I think the angle you want is the angle $QBF.$

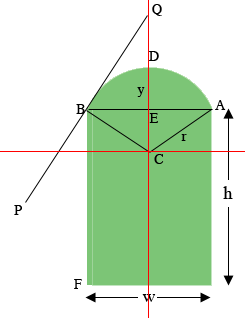
Triangle $EBC$ is a right angled triangle, the length of $EB$ is w/2 and the length of $BC$ is $r$ and hence by Pythagoras Theorem

\[|CE|^2 = |BC|^2 - |EB|^2 \mbox{ or } |CE| = \sqrt{r^2 - \left(\frac{w}{2}\right)^2}.\]

Hence the co-ordinates of $B$ are $\left( -w/2, \sqrt{r^2 - {w^2}/4}\right).$

From this the slope of the line $CB$ is

\[\frac{\sqrt{r^2 - {w^2}/4}}{-w/2}\]

The key to this question is that the lines $QP$ and $CB$ are perpendicular since $CB$ is a radius of the circle an $QP$ is tangent to the circle at $B.$ Since $QP$ is perpendicular to $CB$ its slope is the negative reciprocal of the slope of $CB$ and hence

\[\mbox{ slope of QP is } \frac{w/2}{\sqrt{(r^2 - {w^2}/4)}}.\]

But the slope of $QP$ is the tangent of the angle $QBE$ and hence

\[\mbox{angle QBE} = \tan^{-1}\left(\frac{w/2}{\sqrt{(r^2 - {w^2}/4})}\right)\]

where this time I am going to calculate the measure of the agile in degrees. Finally the measure of the angle $QBF$ is $90^{o} + \mbox{ angle } QBE.$

I have modified the spreadsheet to include the angle measurement and attached it for your use. If you want $H$ to be 69 inches just change the $H$ value in the spreadsheet to 69.

Let me know if this is not the angle you want or if I can be of any further assistance.

Harley