Hi Riley,

The key to solving this problem is the fact that the equation of the circle with center $(h, k)$ and radius $r$ is

\[(x-h)^2 + (y-k)^2 = r^{2}.\]

This might seem to be just another formula to remember, but it's not. It is just Pythagoras Theorem. My diagram below is an illustration of this when the circle lies in the first quadrant.

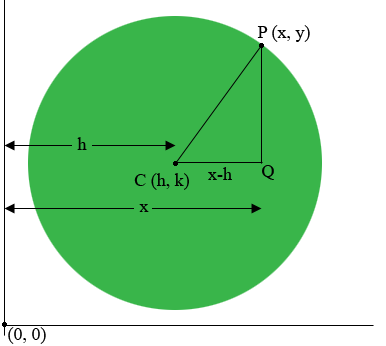
$P$ is a point on the circle, $C$ is the center of the circle, and $Q$ makes $CQP$ a right triangle. The distance from $C$ to $Q$ is $x - h$ and likewise the distance from $Q$ to $P$ is $y - k.$ Since the distance from $C$ to $P$ is $r,$ Pythagoras Theorem gives

\[(x-h)^2 + (y-k)^2 = r^{2}.\]

Applying this to your problem, since $11^2 = 121$ your equation can be written

\[(x - 0)^2 + (y - 6)^2 = 11^{2}.\]

I hope this helps,
Penny