Hi Rob,

In my diagram $w$ is the width of the hexagon (in your case $w = 8$ feet), and $s$ is the side length.

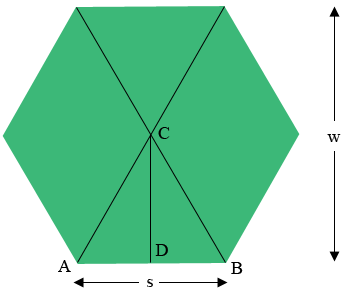
Triangle $ABC$ is an equilateral triangle so the measure of angle $DBC$ is $60^{o}.$ The tangent of the angle $DBC$ is $\large \frac{|CD|}{|DB|}$ and the tangent of $60^o$ is $\sqrt{3}.$ hence

\[\tan(60^{o}) = \sqrt{3} = \frac{|CD|}{|DB|} = \frac{w/2}{s/2} = \frac{w}{s}.\]

Hence $w = s \sqrt{3}.$ Thus in your situation

\[s = \frac{w}{\sqrt{3}} = \frac{8}{\sqrt{3}} = 4.6 \mbox{ feet}\]

Penny