| |||
| Math Central | Quandaries & Queries |
|
Question Sephy: Question 4: Two bags, 1 and 2, each contain equal size counters. A counter is drawn at random from bag 1 If the counter from bag 1 is pink, the number on the If the counter from bag 1 is yellow, the number on the If the counter from bag 1 is white, the number is halved. Find the probability of scoring a number below 3
|
Hi Sephy,
This probability experiment is a two step process and I would examine it with a tree diagram. I have started the tree diagram below.
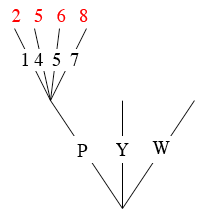
In the first step of the experiment you choose one counter from the first bag and it is either pink, yellow or white. That gives the first level in the tree. The second step is to select a counter from the second bag and the counter is labeled 1, 4, 5 or 7. This gives the second level of the tree. In my diagram I only showed one collection of branches at the second level.
A path trough the tree is a selection of a counter from the first bag and then a counter from the second bag. At the end of each path I have written the result of the calculation in red. In the paths I have included this calculation is to add 1 to the counter from the second bag.
Complete the tree.
Since you a drawing from each bag at random each path through the tree has the same probability. How many paths through the tree are there? How many of these paths have a number less than 3 at the end? What is the probability of taking a path which results with a number less than 3 at the end?
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.