Hi Solon,

I'm not sure I can be of much help. You describe the surface as being uneven and give the heights at the four corners. Unless I know a mathematical description of the surface I can't mathematically determine the volume. The best I can do is give you a rough approximation.

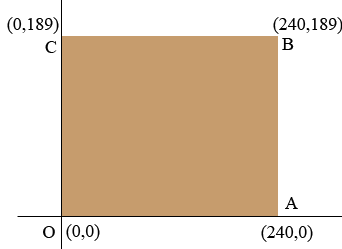
I put a coordinate system on the floor with the origin at the origin, as in the diagram above. Suppose the depth at $A$ is 1 inch and the depth at $C$ is 2 inches. If the surface were a plane then the height at $B$ would be 3 inches, but it's not, it's 4 inches. If the surface were a plane then the volume of fill would be the area of the base (the length times the width) times the height at the center of the floor. The height is 1 inch at $A$ and 2 inches at $C$ and the center of the floor is half way along the line from $A$ to $C.$ The height at this point is the average of 1 inch and 2 inches which is $\large \frac{1+2}{2} \normalsize = \large \frac{3}{2}$ inches. Hence the volume of fill would be

\[240 \times 189 \times \frac{3}{2} \mbox{ cubic inches.}\]

I hope this helps,
Harley