Hi,

I'm going to show you a slightly different problem but hopefully it will help in solving the one you sent. I want to work is base 5 so the symbols are 0, 1, 2, 3, 4. Part A is to create a multiplication table. Here is what I get. (All the numbers should b written with a 5 subscript.)

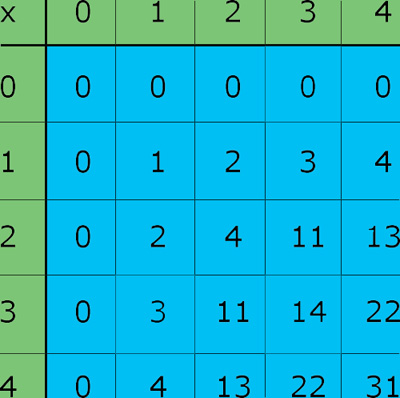
The zero rows and columns and the 1 rows and columns are easy to fill in. Let's do a couple more.

Two times two is four and four written in base five is $4_{5}.$
Two times four is eight and eight is five plus 3 so eight written base five is $13_{5}.$
Four times four is sixteen and sixteen is three times five, plus one so sixteen written base five is $31_{5}.$

Now I want to use this to calculate $234_5 \times 23_{5}.$

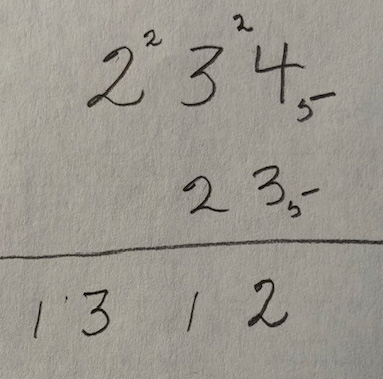
Using the multiplication table above $3_5 \times 4_5 = 22_5$ so write down the units digit, 2 and carry the fives digit, 2. Next $3_5 \times 3_5 = 14_5$ and add the carry of 2 to get $21_5$ so again write down the units digit of 1 and the carry of 2. Finally $3_5 \times 2_5 = 11_5$ and add the carry of 2 to get $13_5$. So the first row in the multiplication of $234_5$ and $23_5$ is $1312_{5}.$

Now the second row

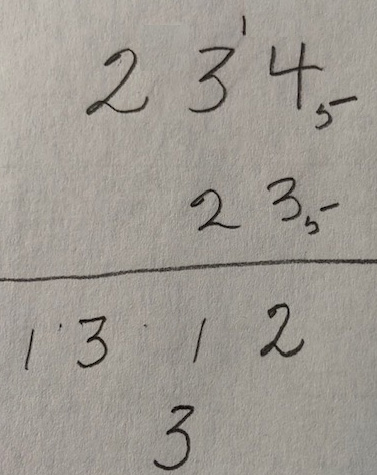
$2_5 \times 4_5 = 13_5$ so shift over one column, write down the units digit of 3 and the carry of 1.

You can complete this row an add to ge the result

\[234_5 \times 23_5 = 12042_{5}.\]

Now try your problem,
Penny