Hi Brian,

I drew a diagram of what I think is your situation.

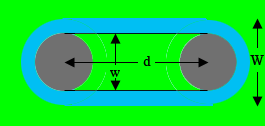
$w,$ lower case W, is the width of the interior rectangle and $d$ is its width. The radius of each circle is $r = w/{2}.$ The film, blue in my diagram, is wrapped around the core.

Is this diagram correct?

Harley

Brian Replied

Hello. That is exactly what I was looking for. I have those variables and the length and thickness of the film. What I'm trying to get is the length and width of the whole thing after the film is rolled on.

The part of the diagram inside the wrapped film is a $w$ by $d$ rectangle and two semicircles of radius $r$ and hence its area is

\[w \times d + \frac{\pi}{4} w^2 \mbox{ square inches.}\]

If $W$ is the width of the wrapped spool as in the diagram then the area of the spool including wrapped film and the region inside it is

\[W \times d + \frac{\pi}{4} W^2 \mbox{ square inches.}\]

The area of the edge of the wrapped spool of film, the race track shaped blue region in the diagram is thus

\[W \times d + \frac{\pi}{4} W^2 - w \times d + \frac{\pi}{4} w^2 \mbox{ square inches.}\]

This simplifies to

\[ d(W-w) + \frac{\pi}{4} \left(w^2 - w^2 \right) \mbox{ square inches.}\]

If the film is of length $L$ inches and its thickness is $t$ inches then one edge of the film can be seen as a long thin rectangle, $L$ by $t$ inches. The area of this rectangle is $t \times L$ square inches. When rolled this long edge forms the blue, race track shaped region in the diagram and hence

\[ tL = d(W-w) + \frac{\pi}{4} \left(W^2 - w^2 \right) \mbox{ square inches.}\]

Rewriting this equation I got

\[\frac{\pi}{4} W^2 + dW - dw -\frac{\pi}{4} w^2 - tL = 0.\]

This is a quadratic equation in $W$ and the general quadratic equation gives

\[W = \frac{2 \left( -d \pm \sqrt{d^2 - \pi \; \left( dw + \frac{w^2}{4} \pi \; + tL \right) } \right)}{\pi} \mbox{ inches.}\]

Choosing the plus sign in front of the square root symbol gives the width with the film wrapped on, and from the diagram the length is

\[d + W \mbox{ inches.}\]

Harley

Brian sent us an example

Example: I start with a 6" diameter core on each side, and I start winding .005" thick film on the core. The distance between the center of those cores, length of the inner rectangle is 7.125. If I continue to do this for a total length of film of 3000 feet, what will the
roll length and width be.

So what I need is the formula to perform this type of calculation.

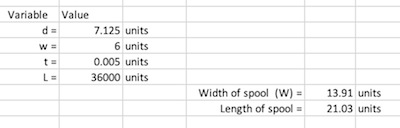
I created an Excel spreadsheet to perform the calculation. In my spreadsheet if you enter the values of $d, w, t$ and $L,$ all in the same units then the length and width of the spool are returned, in the same units. For Brian's example I needed to convert $L$ to inches so I entered $d = 7.125, w = 6, t = 0.005$ and $L = 36000.$

If you would like to use the spreadsheet you can download it here.

Harley