Hi Elias,

Here is a sketch of the football field.

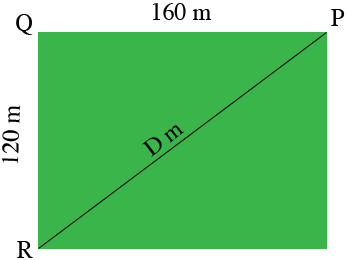
The distance from $R$ to $P$ is $D$ meters. Triangle $PQR$ is a right triangle so by Pythagoras Theorem

\[D^2 = 160^2 + q20^2 \mbox{square meters.}\]

Solve for $D.$

I'm not sure if this is what you want. I think you want to calculate the distance on the scale drawing, so here is my scale drawing.

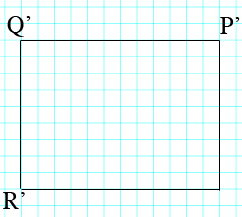
Each 20 meter section of the distance from $P$ to $Q$ on the field is represented by a 1 centimeter along the side from $P'$ to $Q"$ on the scale drawing. What is the distance from $P'$ to $Q'$ in centimeters? What is the distance from $Q'$ to $R'$ on the scale drawing? Use Pythagoras theorem to calculate the distance from $R'$ to $P'?$

As a check on your answer you can use the scale factor to convert the value you found for $D$ into the distance from $R'$ to $P'$ using the scale factor.

I hope this helps,
Penny