Hi Kenneth,

Quite often a rate is between two quantities having different units, for example we often measure the speed at which a car is travelling in miles per hour, or feet per second. A rate can describe the relationship between two quantities that have the same units as sales tax which you mentioned. In this case the rate, which is a fraction, is often reported as a percentage.

For a different example in my house there is a flight of stairs from the first to second floors.

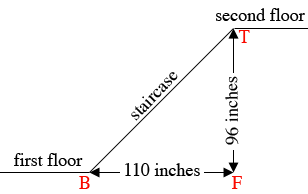
How do you measure the steepness of the stairs? One way is to measure the angle $TBF$ in the diagram and I'll come back to that. Another way is to imagine you are walking up the stairs at a rate of one step per second. You altitude is changing and also your horizontal distance from the base of the stair $B$ is also changing. A measure of how your altitude is changing relative to how your horizontal distance is changing is $\large \frac{96}{110} = 0.873$ inches per inch. This is called the slope of the stairs and is often written as a percent which is 87.3%.

In the triangle $TBF$ the tangent of the angle $TBF$ is $\large \frac{96}{110} = 0.873$ and hence the measure of the angle $TBF$ is the inverse tangent of 0.873, $\tan^{-1}(0.873) = 41.1$ degrees.

I hope this helps,
Penny