Hi Louie,

In my diagram below an octagon is inscribed in a circle with center $C.$ A line is drawn from $C$ to each of the vertices of the octagon to form 8 identical (congruent) triangles. The 8 angles at $C$ have angle measures that add to $360^o$ so each of the 8 angles has measure $\large \frac{360}{8} \normalsize = 45^{o}.$ Thus the angle $BCA$ has measure $45^{o}.$

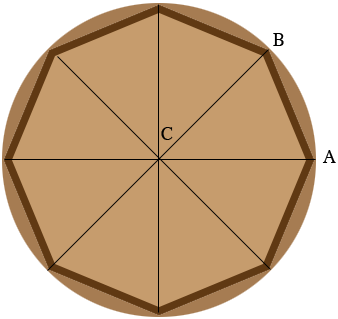
Each of line segments $BC$ and $CA$ are radii of the circle so they are the same length and thus triangle $ABC$ is isosceles. Hence angles $ABC$ and $CAB$ have the same measure. Since the measures of the three angles of a triangle must add to $180^o$ the measure of angle $CAB$ is $67.5^{o}.$ This is the angle to use on your miter saw. Notice that this angle is always $67.5^{o}$ regardless of the width of the octagon.

Now look at triangle $ABC.$ Let $D$ be the midpoint of the line segment $AB.$

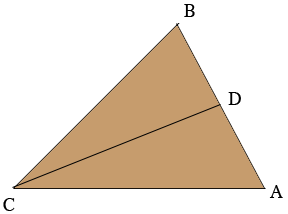
Suppose the radius of the circle is $r$ inches and the side length of the octagon is $s$ inches. Hence $|BC| = r$ and $|DB| = s/2.$ The angle $CDB$ is a right angle and hence, using some trigonometry

\[\cos(DBC) = \frac{|DB|}{|BC|} = \frac{s/2}{r}.\]

Using my calculator $\cos(DBC) = \cos(67.5^o) = 0.3827$ and hence

\[\frac{s/2}{r} = 0.3827\]

or

\[s = 0.765 \times r.\]

Thus for your example where $r = 18/2 = 9$ inches the side length is $0.765 \times 9 = 6.89$ inches. Since $0.89 \times 16 = 14.24, 6.89$ inches is $6$ and $7/8$ inches.

I hope this helps,
Harley