Hi Ruby,

Here is my diagram of Amy's trip. She drove from her home $H$ to grandma's house $H$ on a direct fast route. In the afternoon she drove home on local roads, a more indirect route.

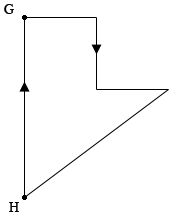
Suppose the distance she travelled to grandma's house was $d_1$ miles and it took her $t_1$ hours, and the distance she travelled from grandma's house to home was $d_2$ miles and it took her $t_2$ hours.

What facts do you know? The total distance she travelled was 300 miles so

\[d_1 + d_2 = 300 \mbox{ miles.}\]

She spent $t_1 + t_2$ hours driving and 2 hours at grandma's house and her total time was 8 hours. Thus

\[t_1 + t_2 + 2 = 8 \mbox{ hours.}\]

On the trip to grandma's house she drove $d_1$ miles in $t_1$ hours and her speed was 70 miles per hour so

\[70 = \frac{d_1}{t_1} \mbox{ or } 70 \times t_1 = d_{1}.\]

Likewise for the return trip we get

\[40 \times t_2 = d_{2}.\]

I would suggest that you solve the first equation for $d_1$ and the second equation for $t_1$ and substitute these values into the third equation. This converts the third equation to one involving $d_2$ and $t_{2}.$ The fourth equation also involves $d_2$ and $t_{2}.$ Solve these two equations for $d_2$ and $t_{2}.$

Penny