Hi Scott,

I drew a diagram of what I think you are describing and added some line segments.

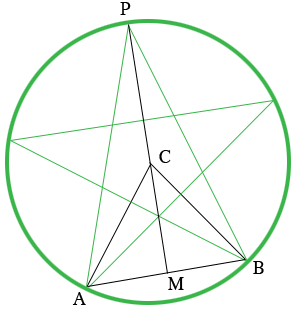
$C$ is the center of the circle and $M$ is the midpoint of $AB.$

By the symmetry of the figure the measure of the angle $BCA$ is $\large \frac{360}{5} \normalsize = 72$ degrees. Again using the symmetry the angle $CMB$ is a right angle and the measure of the angle $BCM$ is $\large \frac{72}{2} \normalsize = 36$ degrees. Also $CB$ is a radius of the circle so its length, $|BC|$ is 7.5 feet.

\[\sin \left(BCM \right) = \sin(36^o ) = \frac{|MB|}{|BC|} \]

Hence you can calculate the length of $MB.$

The cord $AB$ subtends the angle $BCA$ at the center of the circle and the angle $BPA$ at the circumference of the circle and hence the measure of the angle $BPA$ is half the measure of the angle $BCA.$ Thus the measure of the angle $BPM$ is $18^{o}.$

Can you now use the right triangle $BPM$ to calculate the length of $BP?$

write back if you need more assistance,
Harley