Hi Sue,

I drew a diagram of a regular octagon and labeled some vertices and lengths.

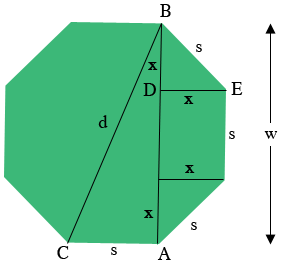
You know the side length $s = 8$ feet and you want to find $d.$ Triangle $ABC$ is a right triangle and the length of $AB$ is $w$ feet, thus by Pythagoras Theorem

\[d^2 = s^2 + w^{2}.\]

Hence if you know $w$ you can solve the above equation for $d.$ Hence all that remains is to find the value of $w.$

From the diagram $w = s + 2 \times x$ and hence we need the value of $x.$ The triangle $EBD$ is isosceles and a right triangle and thus, using Pythagoras Theorem again

\[s^2 = 2 \times x^{2} \mbox{ or } x^2 = \frac{s^2}{2}.\]

Now you are done. Use the equation above to determine $x,$ use this value to calculate $w = s + 2 \times x,$ and then you can use the first equation to determine $d.$

Write back if you need more assistance,
Penny