Hi Aiden,

I drew a diagram of the situation you described. The line $CA$ is vertical and I drew a horizontal line from the base of this line, $C,$ to meet the diagonal at $B.$

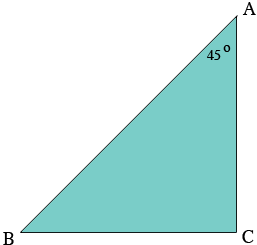
The interior angle of the triangle at $C$ is a right angle and the sum of the interior angles of any triangle must be $180^o$ henge the interior angle at $B$ must measure $180^o - (90^o + 45^o) = 45^{o}.$ Hence the triangle is isosceles and the length of $BC$ and $CA$ are equal.

You suggested using the length $CA$ as 1 inch so the length of $BC$ would also be 1 inch. Since the triangle is a right triangle Pythagoras Theorem tells us that the square of the length of $AB,$ the hypotenuse of the triangle, is the sum of the squares of the length of $BC$ and $CA.$ Thus

\[\left( \mbox{The length of AB}\right)^2 = 1^2 + 1^2 = 2\]

and hence

\[\mbox{The length of AB} = \sqrt{2}.\]

If the length of $CA$ is any other length it helps to use a little algebraic notation to reduce the amount of writing.

Suppose the length of $CA$ is $x$ units then we know that the length of $BC$ is also $x$ units. Suppose the length of $AB$ is $h$ units the by Pythagoras Theorem

\[h^2 = x^2 + x^2 = 2 \times x^{2}.\]

thus

\[h = \sqrt{2 \times x^2} = x \times \sqrt{2.}\]

I hope this helps,
Penny