Hi Javar,

Combination is a technical word in mathematics so I am going to refer to your examples as strings of letters, each string being 12 letters long and only containing the letters A and B.

Sometimes a productive approach to a problem is to consider a smaller problem and examine it. In this case by smaller problem I am thinking of shorter strings. Lets start with the case of strings that are only 2 letters long and again containing only the letters A and B. There are only 2 of them. A and B. Here they are displayed.

What about strings of length 2 letters? Reading from left to right, each string of length 1 can be extended to a string of length 2 by adding either an A or a B. Here are the strings of length 2.

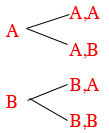
Each string of length 2 can be extended to 2 strings of length 2 and hence there are $2 \times 2 = 2^2 = 4$ strings of length 2.

What about strings of length 3 letters? Each of the strings of length 2 can be extended to a string of length 3 by adding either an A or a B so there are $4 \times 2 = 2^2 \times 2 = 2^3 = 8$ strings of length 3. Here they are.

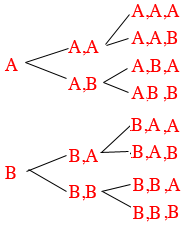
How many strings are there of length 12?

Penny