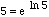Andy

How do you raise a number to an imaginary/complex power? I know how you raise "e" to a complex power, like e^(pi*i): cos pi + i * sin pi But what about numbers other than "e"? What if I want to raise 5 to the 2i power? How is that done?

There is a short answer to your problem and then a complication

Short answer:

Since, by the definition of the natural log, 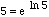(where ln 5 is approximately 1.6094379124341) any power of 5 can be written as a power of e. So

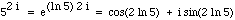. 2 ln 5 is approximately 3.219 and the sine and cosine are straightforward for real numbers, thus 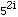is approximately

-0.997 - 0.077i.

Complication:

For any integer k, ,

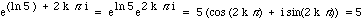thus 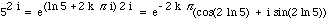. So it makes sense to raise 5 to the power 2i but the answer is not unique.

You can in fact raise any complex number to a complex power. To raise an arbitrary complex number z to the power x + iy (with x and y real), first write z in "polar form": 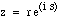where r and s are real numbers. Raising that to the x+iy, and ignoring the non-uniqueness of the answer, we get

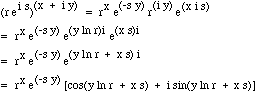
-- Chris