My niece and I were discussing geometry. We'd like to know what practical applications for the Pythagorean theorem may be. I don't often have a need to calculate the height of a mountain. Is there something closer to home?
Thank You
The most widely quoted "practical" application of the Pythagorean theorem is actually an application of its converse. The theorem of Pythagoras says that if a triangle has sides of length a, b and c and the angle between the sides of length a and b is a right angle, then a^2 + b^2 = c^2. The converse says that if a triangle has sides of length a, b and c and a^2 + b^2 = c^2 then the angle between the sides of length a and b is a right angle. Such a triple of numbers is called a Pythagorean triple, so 3,4,5 is a Pythagorean triple and so are 6,8,10 and 5,12,13.
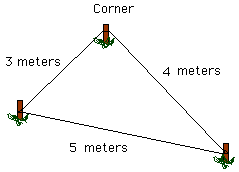
The application is in construction. It is very important when starting a building to have a square corner, and a Pythagorean triple provides an easy and inexpensive way to get one. Drive a stake at the desired corner point and another stake 3 meters from the corner along the line where you want one wall of the building. Then position a third stake so that its distance from the corner is 4 meters and the third side of the triangle formed by the three stakes is 5 meters. Since 3,4,5 is a Pythagorean triple the angle at the corner is a right angle.

As a mathematician I think that an application of a theorem to some area of mathematics is "practical". The Pythagorean theorem is a starting place for trigonometry, which leads to methods, for example, for calculating the heights of mountains. The Pythagorean theorem is also an example of the somewhat rare situation where both the theorem and its converse are true. It is also useful in calculating distances. Suppose you leave home and drive 12 kilometers west then 5 kilometers north. How far are you from home "as the crow flies"?
Cheers,
Penny and Maxine
To return to the previous page use your browser's back button.