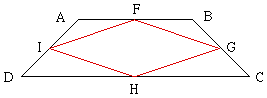
Hello, I have a problem. I doubt you can help me. If you have an isosceles trapezoid, and you connect the midpoints of the four sides of the isosceles trapezoid forming a quadrilateral, how do you prove that it's a rhombus in a 2 column proof??

You doubt that I can help you!! Just read on.

I have labeled the trapezoid ABCD with AB and CD parallel, and |AD|=|BC|. The midpoints of the sides are F,G,H and I as in the diagram.

I want to show that FGHI is a rhombus, that is that the four sides are of equal length. My proof is in three steps.

Step 1:

Angle ADC = Angle DCB

Proof:

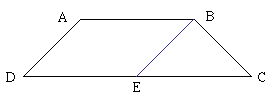
Draw a line through B parallel to AD meeting DC at E. ADEB is a parallelogram so |AD|=|BE| which is also |BC|. Thus triangle BEC is isosceles and angle BEC = angle DCB. Since AD is parallel to BE angle ADC = angle BEC. Thus Angle ADC = Angle DCB.

Step 2:

|AC|=|DB|

Proof:

Using step 1 and side-angle-side, triangles ADC and BDC are congruent.

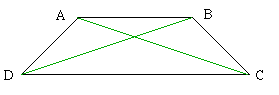
Proof of the main result:

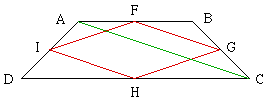
Join A to C. In triangle ABC the line FG joins the midpoints of two of the legs so |AC|=2|FG|. Similarly, using triangle ADC, |AC|=2|IH|.

If you now join B to D, a similar argument shows that |BD|=2|IF|=2|HG|. Since, by step 2, |AC|=|DB|, |FG|=|IH|=|IF|=|HG|.

Cheers

Penny Nom