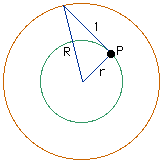
Two cocentric circles form an annulus. The two circles are joined by a segment of length 1" which is tangent to the inner circle. Find the area of the annulus. Show your work.

If the radius of the larger circle is R and the radius of the smaller circle is r then, looking at the figure and using the fact that the angle at P is a right angle, we can see that R^2 = r^2 + 1^2, or R^2 - r^2 = 1. The area of the annulus is given by A = pi*R^2 - pi*r^2 = pi*(R^2 - r^2) = pi.

One of the people here at Math Central, when he saw your problem, did something different. His intuition somehow told him, correctly, that the answer might not depend on the size of the circles. If that is true then suppose that the inside circle has a very small radius, close to zero. Then the line segment of length 1 which joins the circles is very close to a radius of the large circle, and the area of the annulus is approximately the area of the large circle which is approximately pi. His reasoning then said that if the answer to your problem doesn't depend on the size of the circles, the answer must be pi. This is, of course, not a valid solution to your problem but is it an illustration of the fact that sometimes looking at a particular instance of a problem can yield insight.

Penny