What are fractals and are they of any practical use?

Hi Ron:

Benoit Mandelbrot coined the word "fractal" to describe the boundary of a plane region that is so jagged that it cannot be studied by conventional methods of geometry. No formal definition of the concept has been agreed upon, even after more than 30 years of intensive study by leading mathematicians. To obtain an idea of what is involved, Mandelbrot suggests considering the problem of determining the "exact" length of the boundary of a lake. A geographer would do it by drawing the shoreline as a smooth curve and measuring the length of the curve. But a shoreline is not smooth -- if the geographer went around the lake with a metre stick he would get a much larger estimate of the length; a foot ruler would give yet a larger answer, and a micrometer yet larger. One soon concludes that the question of an exact length has no unique solution: the length of the boundary becomes arbitrarily large as the measuring tool becomes sufficiently accurate.

The easiest model of the phenomenon is the infinite process that begins with a unit segment AB and replaces the middle 1/3 by a ^-shaped detour consisting of two segments, CD and DE, each of length 1/3.

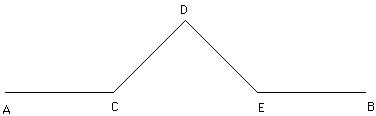
The new path from A to B (going from A to C to D to E to B) has length 4/3. Next replace the middle 1/3 of each of these four segments by a ^ to obtain a path of length (4/3)*(4/3) = 16/9.

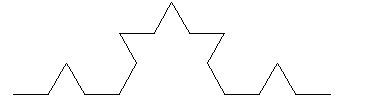
This process, continued ad infinitum, leads to a path that (like the shoreline of a lake) has an "infinite length."

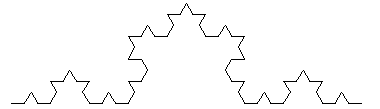
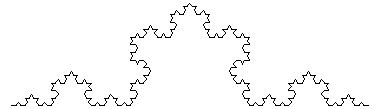
Any definition of fractal must come to grips with the notion of "self-similarity": surround any point of the boundary by a small circle of radius r, and enlarge the figure by the factor 1/r (so that the circle becomes a unit circle). If the boundary is "smooth," the enlarged portion looks like a straight line when r is small enough; if the boundary is "fractal" then it has the same amount of jaggedness when enlarged -- it is "similar to itself" at all levels of magnification. The difficulty with such a definition lies in formulating a precise measure of jaggedness that applies to all objects that one would want to label "fractal."

There are many objects that occur in nature whose boundary can be considered a fractal. The idea is to make use of computer simulation to model such boundaries. Probably the place to read about it is Mandelbrot's THE FRACTAL GEOMETRY OF NATURE; there are a couple books by Heinz-Otto Peitgen et al. that offer an elementary introduction. (Most books that I've seen use quite sophisticated mathematics).

Chris