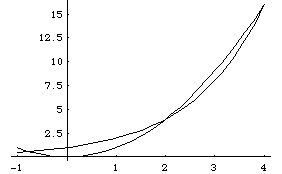
The intersecting points of y=2^x and y=x^2, graphed along with x^2=2^x, are abviously three ... (2,4), (4,16), and (?,?). I am having problems figuring out the value, and even an equation for, the (?,?). Can you help me?

Thanks,

Darin S.

Your observation that there are three solutions is correct. A graph of the two equations for x between -1 and 5 shows the two intersection points you found and another for some value of x between -1 and 0.

A closer look at the graph between these limits shows that the intersection point is somewhere close to x=-0.8.

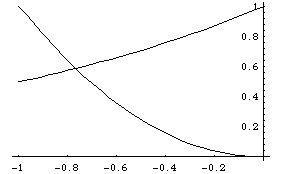
Unfortunately there is no "equation" for this value and the best I can do is approximate it. I will show you two approximation methods.

For the bisection method I will let f(x) = x^2 - 2^x so we are looking for a number t that makes f(t)=0. We already know that the required value is in the interval between -1 and 0 since f(-1)= 0.5 and f(0) = -1 .

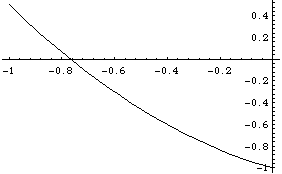
A first approximation for the solution to f(x)=0 might then be half way between -1 and 0, that is x1=-0.5. Now f(x1) = -0.457 (see the graph) and thus we see that t is in fact between -1 and -0.5. Continue by taking x2 = -0.75.

In general at each step you do the following:

1. t is in an interval between a and b with f(a) positive and f(b) negative. Let xj=(a+b)/2 and evatuate f(xj).
2. • If f(xj) is positive then t is between xj and b so let a=xj and return to step 1.
   • If f(xj) is negative then t is between a and xj so let b=xj and return to step 1.

The values obtained for xj are successively better and better approximations to t. After 10 iterations I got a value of x10 = -0.76709 and f(x10)=0.000826. After 20 iteration, x20=-0.766665 and f(x20)=0.000000555. So the true value of t is approximately -0.766665.

Using a knowledge of the natural log and exponential functions there is another technique that arrives at a similar approximation in fewer steps.

To be able to work with positive numbers, rewrite the equation as
1 = (2^x)*(x^2) for x > 0. Take the log of both sides and "solve" for x:
0 = x*(ln 2) + 2*(ln x)
ln x = -(ln 2)/2 * x

Finally, letting r = -(ln 2)/2,

x = e^(rx).

One way to estimate the solution t by calculator is to first store the value r and then perform the algorithm:
input x, multiply by r, and then raise e to that power to get the next x-value:

x --> r*x --> e^(rx) -->x repeat

As an initial guess, input x=.7. After 10 or so repetitions you will get x=.7666647, which gives the correct solution to 6 significant digits. (The reason the method works is that the derivative of e^rx has absolute value less than 1 around x=.7.)

Cheers Harley