Like your problem. It's actually been around for a long time - it was one of the puzzles in Henry Ernest Dudeney's book published shortly after he died in 1931 - but I'm not sure of its origin.

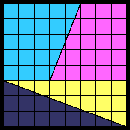
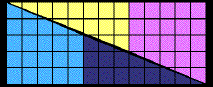
The problem is actually an illusion. If you look closely at the following diagrams in which the parts have been carefully measured you will notice a thin `diamond shaped' white region in the 5 by 13 rectangle. Its area is exactly one - the missing one in your puzzle. What is really happening is that the yellow and blue regions don't really make a triangle that is half of the 5 by 13 rectangle. If you were to very carefully extend the slanted edge of the pink region it would only get up to 12.5 (not 13) steps on the right hand edge of the large rectangle. That is, the edge of the pink region and the diagonal edge of the yellow region don't make a straight line. Very close, but not quite. The result is that when we hand-draw the diagrams (or use cut outs) this thin white parallelogram (the `diamond shaped' region) is hard to see.

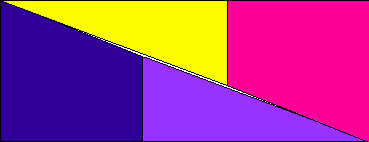
At first glance it seems like the total area has become (5 x 5) + (1 x 13) + (5 x 5) = 63 but careful inspection will show an overlap of area precisely one.

You can play these tricks with squares of many different sizes, not just the 8 by 8. You could use any three consecutive terms of the following sequence if you like: 3, 5, 8, 13, 21, 34, ... . For example, starting with a 13 by 13 square, if you make and rearrange coloured regions similar to the ones you sent me, the resulting rectangle is an 8 by 21. The square has area 169 but the rectangle has area only 168! Try other terms from the sequence. By the way, do you see how this sequence of numbers continues?

There is a version of Dudeney's book published by Scribners & Sons. It's called 536 Puzzles & Curious Problems, H. E. Dudeney, Edited by Martin Gardner, SBN 684-71755-7. Perhaps your school or your nearest library has a copy.

Now a problem for your class. Suppose when you run up stairs you always take them in 1 or 2 steps at a time. I'd like you to tell me in how many different ways you can run up a flight of 5 stairs? Here for example you could run up the stairs in steps 2-2-1 or 2-1-1-1 or 1-2-1-1 and so on. What if there were 10 stairs? Or 20 stairs?

Denis