Name: Nathan
Who is asking: Student
Level: Secondary

Question:
Picture a 9 inch diameter circle. Inside that circle is a 6 inch diameter circle tangent to it. Then, tangent to both circles is a 3 inch diameter circle. So there are three circles, two smaller ones inside a big one, all of them just touching but not overlapping.

Now picture a chord on the 9 inch circle that is created by making a line that is tangent to both the 6 and the 3 inch circles and extending it to the edge of the 9 inch circle.

I need the length of that cord. I know it is about 7.5 inches, and I have tried a number of different ideas but I can't seem to get a solution. I'm fairly sure I have to extend the center line of all three circles (the diameter line) out (1 line for all three circles), and extend the chord to intersect it, but I'm not sure what to do with that.

Thanks a lot!

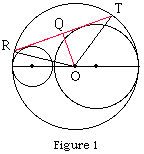
Let O be the center of the large circle and R and T the points where the chord meets this circle (see Figure 1). Draw a line through O perpendicular to RT meeting RT at Q. Let c be the length of the chord RT. Since triangles QRO and TQO are congruent |RQ|=c/2. Since angle OQR is a right angle and |OR|=4.5 we can use the theorem of Pythagoras to find |RQ| if we know |OQ|.

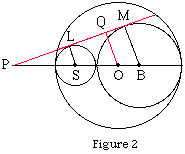Let S be the center of the circle of diameter 3 and B be the center of the circle of diameter 6. Extend the lines TR and BS to meet at P. Let L and M be the points where the two interior circles are tangent to the chord TR (see Figure 2). Using similar triangles |PS|/|PB|=|SL|/|BM|=1.5/3 so 2|PS|=|PB|. But |SB|=4.5 thus |PS|=4.5 and therefore |PO|=7.5. Again using similar triangles |PO|/|PS|=|OQ|/1.5 and thus |OQ|=2.5. Returning to Figure 1 and the right triangle OQR, |QR|^2=|RO|^2-|OQ|^2 = (4.5)^2-(2.5)^2 = 14. Thus c=2|RQ|=2*Sqrt(14) which is approximately 7.5

Cheers
Chris