Name: Paul
Who is asking: Teacher
Level: All
How does one calculate the volume and the height of a three sided pyramid formed by equilateral triangles?
Hi Paul
The figure you describe is called a regular tetrahedron. It is actually composed of four triangles, the tent needs a floor. Let a be the length of a side of the triangle. In the figure draw a perpendicular line from V to a point D in the base.
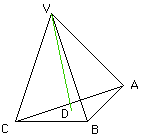
Look at the base and draw a line through B and D to meet the side AC at P and a line from A to D to meet the side BC at Q.
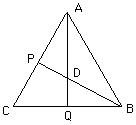
Using the symetry in this figure, the line AQ bisects the angle CAB, the thus angle PAD is 30 degrees and the angle ADP is 60 degrees. In any 30-60-90 triange the lengths of the sides are in the ratios 1:2:sqrt(3), hence we know that AD is twice as long as PD and, again by the symetry, AD is twice as long as DQ. (I am using sqrt for square root and * for multiplication.) Now triangle ABQ is a right angled triangle with AB of length a and QB of length a/2 and thus, using the Theorem of Pythagoras, the length of AQ is (sqrt(3)/2)*a. Thus AD is of length (sqrt(3)/3)*a.
Back in the first diagram the vertical triangle VDA is also a right angled triangle with VA of length a and AD of length (sqrt(3)/3)*a so, by the Theorem of Pythagoras again, VD has length sqrt(2/3)*a. This is the answer to one of your questions, what is the height of the regular tetrahedron?
The volume can be determined by the fact that the volume is (1/3)*(the area of the base)*(the height). Looking at the second diagram the base has area (1/2)*a*AQ so the volume simplifies to (sqrt(2)/12)*a3.
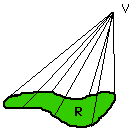
I don't know an easy proof that the volume is (1/3)*(the area of the base)*(the height). It follows from a much more general result that says if you take some region R in the plane with an area, some point V not in the plane and form a cone by joining every point on the boundary of R to V with a straight line then the volume of the cone is (1/3)*(the area of the base)*(the height).
Bruce Gilligan.