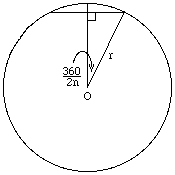
Date: Tue, 29 Oct 1996 14:34:52 -0800
From: "Quandries and Queries Consultants
Sender: Ben 
Organization: H&L Management Systems

if you take a unit circle (centred at 0,0) then the distance between the points of intersection with the +ve x and y axes is root 2, and the length of the arc (that is the quarter of the circle in the +ve quadrant) is Pi/2. Is there some way of using this relationship to calculate Pi?

any help much appreciated

Ben.

Archimedes, who flourished around 250 BC, was the first to estimate pi in a systematic way. His work can be found on pages 91-98 of the paperback version of Heath's translation. It is so well written that a high-school student would be able to read it. Proposition 3 says that The ratio of the circumference of any circle to its diameter is less than 22/7 (= 3.1428...) but greater than 223/71 (= 3.1408...).

Call the circumference c. Archimedes' idea was to circumscribe a regular n-gon about a circle. If n is a large number, the perimeter of the n-gon would be a tiny bit larger than c because the circle is trapped inside. Next inscribe a regular n-gon in the circle and note that when n is large the perimeter of the n-gon will be a tiny bit smaller than c. Since c is between two numbers that are very close together, those numbers must each be a good estimate for c. Archimedes got his upper and lower estimates by using n = 96. Why a 96-gon? Because he was extremely clever!

Before looking at what Archimedes did, let's use our knowledge of trigonometry to find the perimeters of the two n-gons.

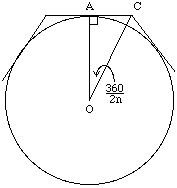
	To get the outside perimeter of a regular n-gon, use the right triangle formed by the radius r=OA to the point of tangency A, half the polygon's edge AC, and half the diagonal CO. The angle at O is (360 degrees)/(2n) so AC = r tan(360/(2n)). An edge is twice AC so that the ratio of the perimeter to r is 2n tan(360/(2n)).
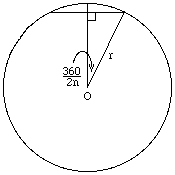	The inside right triangle leads to the ratio of the inside perimeter to r, which is 2n sin(360/(2n)). Using your calculator with n=96 you get the estimates 3.142 (the perimeter of the outside n-gon) and 3.141 (form the inside n-gon).

Here is how Archimeded managed these calculations without a calculator and without trig tables. (Trig tables might have been computed in the next century, but the first tables known to have existed are those of Ptolemy some 400 years later!) He bagan with a regular hexagon for which the measurements are simple: AOC is a 30-60 right triangle so that tan (360/12)=tan 30 = 1/sqrt(3) and sin 30 = 1/2. The most important number in the calculation turns out to be cos 30 = sqrt(3)/2. Now double the number of sides, which means the angle at the center becomes 30/2 = 15 degrees. By the half angle formula (perhaps discovered by Archimeded himself) sin(a/2) = sqrt((1-cos a)/2) and tan(a/2) = sqrt((1-cos a)/(1+cos a)), so all that's needed is cos(a/2) = sqrt((1+cos a)/2). Now compute cos(360/24) = sqrt((1+sqrt(3)/2)/2), cos(360/48) = sqrt((1+cos(360/24))/2), ..., cos(360/192) = sqrt((1+cos(360/96))/2).

Nobody improved on this work until the advent of calculus in the 17th century. The story is told in the accessible book A History of Pi by Peter Beckmann. There is also an interesting article in Mathamatics Magazine 61(numbers 2 and 3) (1998) 67-98 and 148-163: parts of this article are elementary and parts are not.

Chris