Who is asking: Student
Level: Secondary

Question:
How do I find the foci of the following equation? 4x^2 + 9y^2 = 36.

Thank you, David

By the form of the expression I know that it is an ellipse, and an ellipse is the locus of points such that the sum of their distances from two fixed points is a constant which I am going to call k. The fixed points are called the focii.

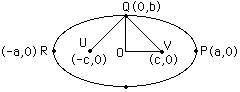
In the diagram U and V are the focii. Since P is on the graph |UP|+|VP|=k. By the symmetry |VP|=|RU| so the distance from R to P is k. Thus k=2a. Since Q is on the graph |UQ|+|QV|=k=2a, but |UQ|=|QV| so |QV|=a. Thus QOV is a right angled triangle with sides of length b and c and hypotenuse a. In your example when y=0, x=+/-3 thus a=3 and simularily b=2. Thus, using Pythagoras Theorem for the triangle QOV, c=sqrt(5).

Cheers
Harley