To: QandQ@MathCentral.uregina.ca
Subject: Probability

Ok, just one more question. This is Donna Hall, I am a secondary ed. mathematics teacher. This question came up in my graduate class and I am a little shaky on how to solve it:

A irregularly shaped object of unknown area A is located in the unit square 0<=x<=1 (sorry, no inequality symbols available on this e-mail). Consider a random point uniformly distributed over the square. Let X = 1 if the point lies inside the object and X = 0 otherwise. Show that E(X) = A. How could A be estimated from a sequence of n independent points uniformly distributed over the square? How would you use the central limit theorem to gauge the probable size of the error of the estimate.

Can you help me?
Thank you immensely.

Since your irregularly shaped object is inside a square, the probability that your randomly selected point lies inside the object is equal to the proportion of the area of the square that is covered by the object. That is P(X=1) = A and thus P(X=0) = 1-A. Hence
.

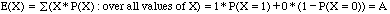The method that you are suggesting for estimating the area A is sometimes called the Monte Carlo method. If n is large and you have "n independent points uniformly distributed over the square" then you have n random variables, 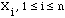, each identical to X and hence, by the Central Limit Theorem, the distribution of 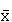is approximately normal with 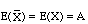. Thus a confidence interval for 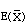gives bounds on the error when using 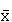as an estimate for A.

Cheers,
Harley