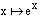 around x = 0. For every positive "whole" number n there is
around x = 0. For every positive "whole" number n there is
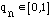 so that
so thatSubject: irrational numbers
Hello!
We have a little mathematical problem... we need some help proving e is an irrational number!
We don't feel very confident in our formulas, so if You have the time to give us a little explanation we would be very grateful!!!
Thank You very much!!
/"Students in trouble" (Peter and Jenny)
We asume that e is an irrational number, that e=(a/b) where a
and b are positive "whole" numbers. We asume that e is an
irrational number, that e=(a/b) where a and b are positive "whole" numbers. By
using the Taylor-method for
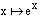 around x = 0. For every positive "whole" number n there is
around x = 0. For every positive "whole" number n there is
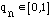 so that
so that
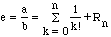 ,
,
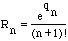
We want to show that b*n!*Rn is a "whole" number for all n 1 and that b*n!*Rn 0 when
n approaches
 .
.
This will be a contradiction. We wan't to know why!!
What you are doing here is correct but you don't need a special form for the
remainder. It is more direct to write
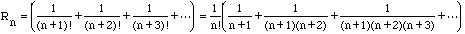
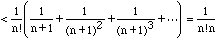 since
since
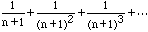 is a geometric series. Thus when n=b,
is a geometric series. Thus when n=b,
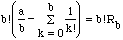 is
an integer but
is
an integer but
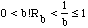 which is impossible.
which is impossible.
Cheers
Doug and Penny
To return to the previous page use your browser's back button.